Fourier's Formula Unifies all of Physics
Connecting signal theory, quantum mechanics and general relativity
Introduction
Meet the unsung powerhouse of mathematical physics: The Fourier transform.
It's the formula that makes the graphical equalizer on your stereo work:
If you've ever dealt with audio production, engineering, physics, or mathematics, you probably already know that the Fourier transform takes a signal from the time domain to the frequency domain, and vice versa.
Joseph Fourier (1768–1830), while working on the heat equation, developed his famous transform around 1807 (at the age of 39):
\(X(f) = \int_{-\infty}^{\infty} \ x(t) \cdot e^{-j2\pi f t} \ dt\)
Mathematically, the Fourier transform is just a bijective operator. It maps one space to another in a unique and reversible way. Yet, it's so much more than just a formula.
In particular, the Fourier transform also plays a fundamental role in quantum mechanics and is thus directly responsible for describing the reality we perceive. So bear with me as I break it down and show how it even connects to Einstein's theory of relativity.
Signal Theory
In signal theory, the Fourier transform maps a signal in the time domain to a spectrum in the frequency domain. In quantum mechanics, the Fourier transform maps a wavefunction in position space to a wavefunction in momentum space.
To get a feeling for the Fourier transform, let's consider the simplest pair of signals: The spike and the constant.
The spike signal is transformed into a constant spectrum. In engineering terms, the spike signal is idealized as an infinitely high voltage pulse (from 0 to ∞ volts and back in an instant) with an infinitely short time duration. The constant spectrum is perfectly flat, reflecting the broad frequency content of an ideal impulse. In reality, an abruptly pulsed voltage signal will approximately have a white noise floor in the spectrum.
Conversely, a spike in the spectrum is transformed into a constant signal, but only if the spike is at DC (zero-frequency); if the spike in the spectrum is not at DC, the signal will oscillate with that frequency.
In general, each point in the spectrum (frequency domain) corresponds to a harmonic component of the signal (time domain). Usually, the points are complex numbers (polar coordinates), encoding both amplitude and phase of the harmonic component.
The infinitely big and short spike signal is also called the Dirac delta distribution.
Quantum Mechanics
When transferred from signal theory to quantum mechanics, we can intuitively grasp Heisenberg’s uncertainty principle: A well-localized function in position space is transformed into a spread-out function in momentum space, and vice versa. It's just the "spike-to-constant" transformation all over again.
Heisenberg's uncertainty relation quantifies the trade-off between the spread of a wavefunction ("a signal in Hilbert space") in position and momentum space, which are related by a Fourier transformation:
\(\Delta x \cdot \Delta p \geq \frac{\hbar}{2}\)
It's kind of poetic, and a bit ironic, that yet another cornerstone of quantum mechanics ties back to the works of Fourier: As it turns out, Schrödinger's equation is mathematically very close to the heat equation, except it deals with complex amplitudes instead of real temperatures.
Schrödinger's equation is basically a heat equation on imaginary steroids. The steroids are called a Wick rotation, where ordinary time t is replaced with imaginary time -iτ. 1
Who would have thought that after Fourier developed his famous equation while working on the heat equation, over 100 years later quantum physicists are still using his formula, except now they've upgraded the heat equation from the complex plane to all of Hilbert space, sprinkled with a dash of Born's rule for that quantum randomness.
After all, Born's rule is just a probablistic interpretation of signal energy.
I think it's safe to say that the Fourier transform is the powerhouse of mathematical physics. But we're not even done just yet: What if I told you there's a natural way to connect quantum mechanics to general relativity, using the discrete Fourier transform as a bridge?
Discreteness and Aliasing
The Fourier transform actually comes in two different flavors: Continuous and discrete. While the continuous version is primarily used in mathematics, the discrete version is more relevant in everyday digital technology — and in physics, apparently.
The discrete Fourier transform turns a discrete signal into a discrete spectrum, and vice versa. In this context, 'discrete' means that a continuous signal or spectrum is sampled at regular intervals, only extracting values of the signal at the sampling points.
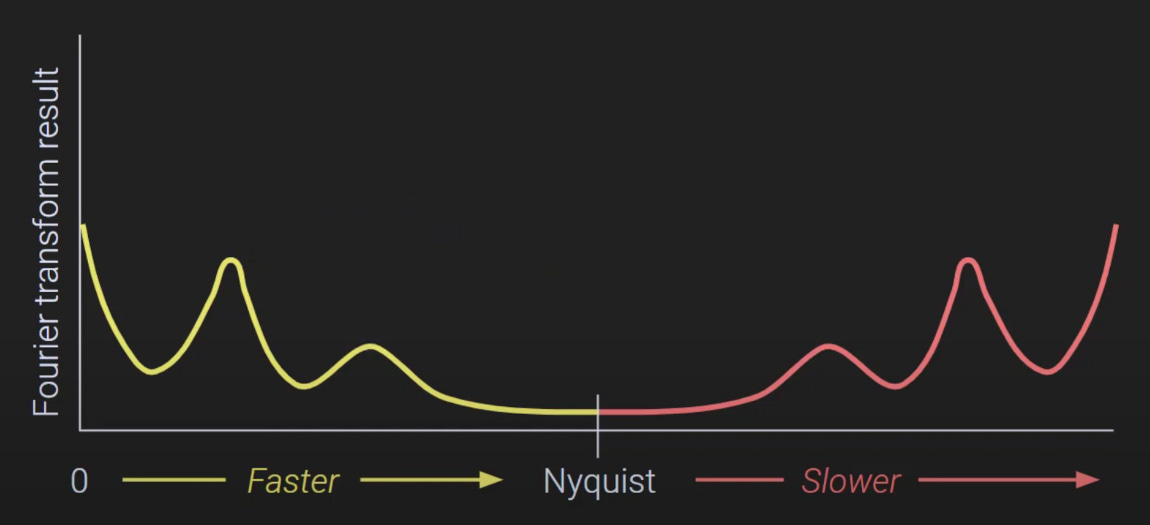
However, sampling at a fixed frequency fS means that there's a limit to the maximum frequency allowed in the original continuous signal. This limit is called the Nyquist frequency fN, and it's exactly half of the sampling frequency:
It's a well-known property of the discrete Fourier transform that a discrete and periodic signal transforms into a discrete and periodic spectrum, and vice versa. The key here is to understand that the spectrum is periodic. Any frequency component above the Nyquist limit gets folded back into the spectrum, appearing at a different (usually lower) frequency — often even as a negative frequency. This effect is called aliasing.
(The above screenshot was Taken from YouTube video "Positive and Negative frequencies" by Mike X Cohen.2)
In digital signal processing, aliasing is an unwanted effect and detrimental to audio or video quality, which is why consumer signals are always low-pass filtered before being sampled and digitized. However, if aliasing could also be shown to appear in the physics of our universe, it would open the doors to very exotic effects.
Ties to Relativity
Within the framework of the discrete Fourier transform, no signal can have a frequency higher than the Nyquist frequency. In Einstein’s universe, no signal can propagate faster than the speed of light. The Nyquist frequency and the speed of light thus represent the natural limits of Fourier’s and Einstein’s respective frameworks.
But what happens when we attempt to break these limits? A frequency component exceeding the Nyquist threshold wraps around the spectrum due to aliasing. Similarly, a signal traveling faster than light would, in a strange way, “wrap around in time.”
In fact, according to the tachyonic interpretation of faster-than-light travel within the framework of general relativity, an object exceeding the speed of light would appear to move backward in time.
Fun fact: In the tachyonic framework, faster-than-light particles (tachyons) are predicted to possess imaginary mass or energy.3 Wait ... imaginary steroids — again!?
Although a rigorous bridge between the discrete Fourier transform and Einstein’s relativity has yet to be built, the parallels are certainly worth appreciating.
Conclusion
There appear to be striking similarities between signal theory, quantum mechanics, and general relativity. The Fourier transform is the basis of all of them. Now it’s our turn to bring them together — perhaps into a grand theory of quantum gravity, grounded in signal and information theory.
In memory of Joseph Fourier (1768–1830) — the genius mathematician and natural philosopher who transformed heat into harmony, and equations into insight.
Join the discussion—please subscribe, comment, retweet, share.
Follow @drxwilhelm on X Twitter, Substack, Bluesky, Discord, and YouTube. (About)
Kerry Welch, The Meaning of Imaginary Time: Creativity’s Dialog with Timelessness (https://textureoftime.wordpress.com/2015/07/15/the-meaning-of-imaginary-time/)
Mike X Cohen, Positive and Negative Frequencies:
Mohammed Abbasi, What are tachyons? (https://mmabbasi.com/2015/03/30/what-are-tachyons/)







I was hoping finally for some insight into how mass/energy/acceleration might emerge from Fourier analysis or quantum mechanics, but this didn't happen.
But the good news is that this post is a good counter to the misunderstanding that Heisenberg's Uncertainty Principle is something physical, not just the basic mathematical nature of measurement and the relationship between a function and its derivative or integral.
Unfortunately, I don't yet have a clear signal theoretic interpretation of the Hamiltonian yet. Is that what you’re asking? In any case, thank you for the feedback (it means a lot to me). Also, please consider subscribing, because I'd appreciate your feedback on future posts as well!