Magnetic Fields hate this Trick
No right-hand rule. No Maxwell. Just clean logic.
Introduction
As engineers and physicists, we all know that magnetic fields come in closed loops. So an image like this won’t surprise us much:
However, the actual reason why the magnetic field appears circular like that is less well known.
That’s why, when a friend once asked me that exact question, I couldn’t give a straight answer. But that was a few years back, and today I’ll finally give it a shot.
Potentials > Fields
First, we need to understand that the magnetic field B (in units of Tesla) itself is not fundamental. Instead, it is derived from the vector potential A (in units of Tesla-meter) by applying the curl operator, “∇×”, which is a sort of spatial derivative:
For any given electrical current density, the vector potential A is obtained by spatially integrating over the current distribution, and the magnetic field B is then obtained by taking the curl of A.
That is, an electrical current (density) doesn’t generate a magnetic field directly; instead, it only generates a vector potential field, from which a magnetic field then naturally seems to arise.
The vector potential is a real entity, not just a mathematical tool; this debate, reaching back to the end of the 19th century, has de facto been settled by positive experimental validation1 of the Aharonov-Bohm effect by R. G. Chambers in 1960. In short, the vector potential shifts the phases of electron wavefunctions, altering the interference patterns of a double-slit experiment in a way that can’t be explained without it.
Straight Wire
Let’s put all of the above into practice now.
Consider a straight wire along the z-direction, carrying a current I. The corresponding vector potential A is given by Feynman2 as:
Since Ax = Ay = 0, the vector potential points in the z-direction only. It is perfectly parallel to the wire, and decays logarithmically with the radial distance:
Note that ln(1/r) becomes negative for r > 1. The curl operator doesn’t care about that, though; you can always shift the potential by rescaling the radial distance, e.g. substituting 1/r by C/r, where C is a constant. In fact, there are infinitely many ways to construct different vector potentials that all yield the same magnetic field. This concept, called gauge freedom, is fundamental to physics.
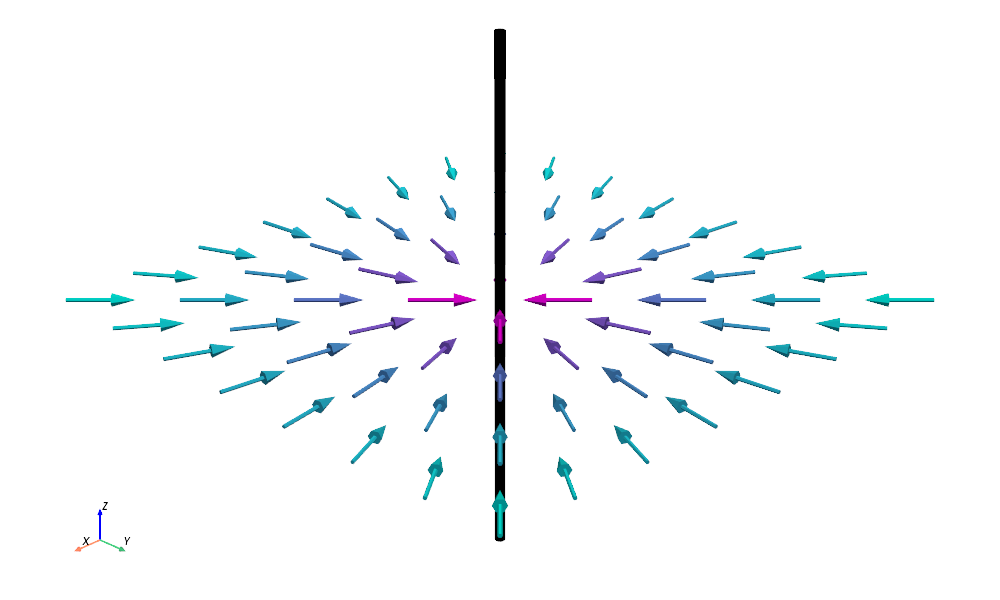
Let’s look at the vector potential field in the xy-plane (at some fixed z along the wire). Doesn’t it almost appear as if the electrons, moving inside the wire, are dragging something with them on the outside? Well, that something is the vector potential!
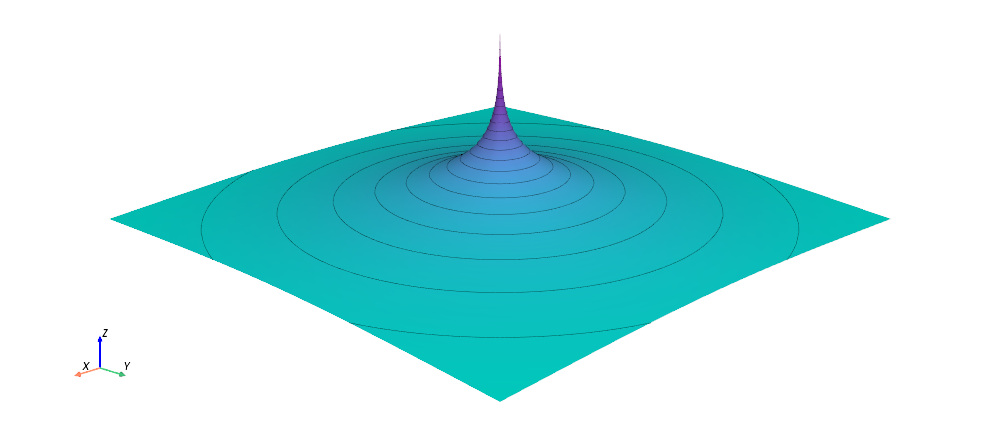
Now, looking at the magnitude of Az, we can see that it is radially symmetric. Imagine the wire having a potential surface like that at every point along its length in the z-direction:
This radial symmetry of Az is our first clue as to why the magnetic field could be circular: Because the isopotential lines of Az are also circular.
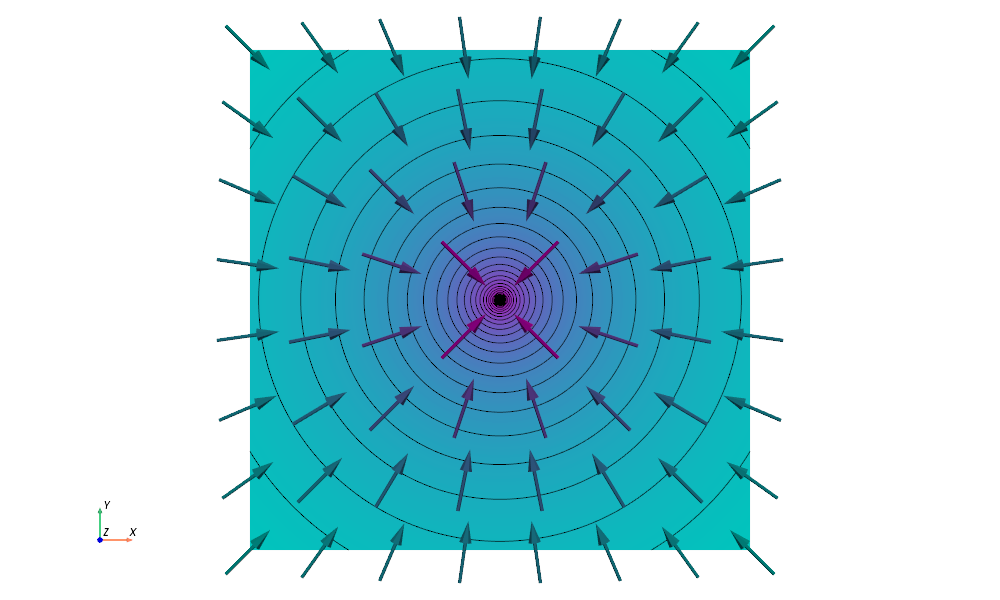
The isopotential lines are lines where Az is constant. Since Az only depends on the radius r, i.e. Az = Az(r), a constant value of Az(r) implies a constant value of r, resulting in circular isopotential lines.
Into the Center
The gradient operator, “∇”, transforms a scalar field into a vector field, where each vector signifies the direction and strength of the steepest incline.
Indeed, Az, being the only non-zero component of the vector potential A, can be treated as a scalar field over the xy-plane, so we can take its gradient:
Just look at the previous image of Az again – there’s a pretty steep rise towards the center (wire). This means that the gradient of Az should also point towards the center. Indeed, it does:
While we’ll skip the full derivation, the gradient of Az works out to:
\(\nabla A_z = \left( \frac{\partial A_z}{\partial x},\ \frac{\partial A_z}{\partial y},\ \frac{\partial A_z}{\partial z} \right) =\ \ldots\ = \left( -\frac{I x}{2 \pi \epsilon_0 c^2 r^2},\ -\frac{I y}{2 \pi \epsilon_0 c^2 r^2},\ 0 \right)\)With a vanishing z-component like that, the gradient of Az is oriented entirely in the xy-plane.
Notice that the gradient of Az is also radially symmetric, because it also only depends on the radius r. Can you already see how this symmetry—pointing straight to the center—could relate to the magnetic field?
We are this close to solving the mystery!
Just a rotation away
In the end, we want to understand the process of deriving B from A. Even though we already know that the “built-in” curl operator does it, let’s think for ourselves for a moment.
The magnetic field should not introduce any new kind of symmetry that’s not already present in the vector potential. Hence, the magnetic field should also be radially symmetric with the radius r, i.e. be oriented in the xy-plane. This is our first assumption, which is physically well-motivated by the radial symmetry.
Now, we need to make one more assumption—this time grounded in experimental fact.
The magnetic field should have no divergence, i.e. it won’t flow into or out of any point.
This assumption is on very good solid grounds. In fact, it’s one of James C. Maxwell’s (1831–1879) famous equations:
\(\nabla \cdot \vec{B} = 0\)Where “∇⋅” is the divergence operator.
Recommended read: Hunting the Hidden Vector
We can readily see that the gradient of Az itself cannot be the magnetic field, as it converges to the center, which is the same as diverging from it. So it has a non-zero divergence, defying our assumption.
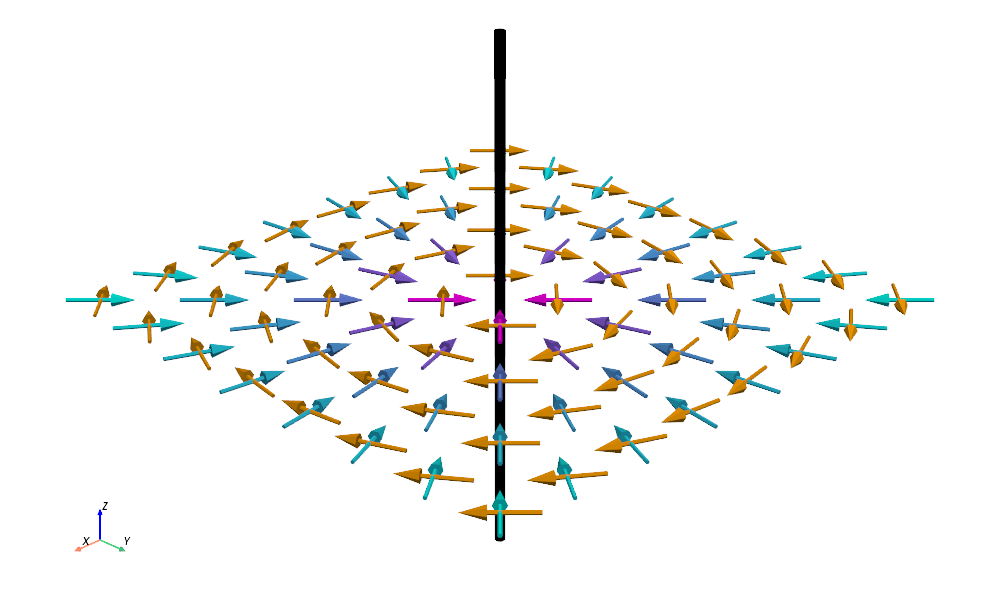
Instead, looking at the gradient of the vector potential, ∇Az, can we rotate it in some direction to make it look like B? The answer may surprise you:
Yes, we can rotate ∇Az, and a simple orthogonal (90°) rotation seems to be the only sensible choice, since we’re limited to the xy-plane per our symmetry assumption.
It’s remarkable how cleanly this works out. Rotating the gradient of the vector potential produces vectors (shown in orange) that match the shape of the magnetic field.
In fact, the orange vectors not only match the shape of the magnetic field, in our example they are identically the magnetic field!
Constructed result
Let’s see if we can prove that. We’ll first calculate the magnetic field B according to our construction above.
We need to use our knowledge of basic vector algebra here:
The cross-product of two vectors yields a third vector orthogonal to both.
Since we know that our orange vectors—let’s call them B′—should be orthogonal to both ∇Az and the z-axis, i.e. be oriented in the xy-plane, this is the valid formula for our orange vectors:
Where (0, 0, 1) is, of course, the unit vector along the z-axis. Our expression then expands to:
Conventional result
Now let’s calculate the magnetic field B again, this time going the conventional way by taking the curl of A, which expands to this:
(Note that I simplified the notation a bit by defining ∂x := ∂/∂x.)
Now, because Ax = Ay = 0, we are left with:
As you can see, in this example, the construction and the conventional curl calculation yield the same result:
Conclusion
We start with the vector potential of a straight wire (which is calculated from the electrical current density in the wire). Realize that its only non-zero component lies in the z-direction of the wire, so we can treat Az as a scalar field over the xy-plane.
Realize that the scalar field Az is radially symmetric, i.e. it has circular isopotential lines. Its gradient points inward and inherits that symmetry:
The magnetic field must follow the symmetry of the vector potential, i.e. also be radially symmetric, hence be oriented in the xy-plane. Rotating the gradient vectors by 90° in the xy-plane is the only natural way to obtain a divergence-free field:
Voilà, enjoy your magnetic field, which we constructed from its cause—the current density—via its proxy, the vector potential, based on arguments of symmetry.
In this example of the straight wire, its magnetic field is tangent to the gradient of its radially symmetric vector potential.
And this is why the magnetic field is circular. We found it—not from Maxwell, but from symmetry.
Even though I would’ve loved to avoid assuming vanishing divergence entirely, the resulting argument is remarkably coherent. And I’ve not seen this being discussed anywhere else. This is what they don’t show you in physics class—but absolutely should.
If anyone’s seen this line of reasoning explored elsewhere, I’d love to know.
Join the discussion—subscribe and comment below.
Follow @drxwilhelm on X Twitter, Substack, Bluesky, Discord, and YouTube. (About)
The source code used to generate the graphics in this article is in the public domain.
Chambers, R. G., Shift of an Electron Interference Pattern by Enclosed Magnetic Flux, Phys. Rev. Lett. 5, 3–5 (1960), DOI:10.1103/PhysRevLett.5.3.
The Feynman Lectures on Physics, New Millenium Edition, Volume II, eq. (14.21).






You're on to something 🌀