Dirac Got Away With Breaking the Rules
On the hidden vector field behind magnetic monopoles
Magnetism: Do's and don'ts
Have you ever heard about magnetic monopoles? It’s what you thought you’d get when you break apart a bar magnet as a little kid.
The bar magnet is a dipole (2-pole), because it has 1 north and 1 south pole. A magnetic monopole would be … well … a mono-pole, having 1 north or 1 south pole.
However, ordinary nature doesn’t seem to like the idea of monopoles so much. In fact, James C. Maxwell (a.k.a. the godfather of electrodynamics, 1831–1879) expressed this fact mathematically more than 150 years ago. Heaviside (1850–1925), both a genius engineer and mathematician, later invented modern vector calculus and stepped in to re-express it as:
(Where "∇·" is the divergence operator and B is the magnetic field.)
Actually, Maxwell would likely spin in his grave if he knew what theorists did to his theory in the meantime. Today, on the hunt for physics beyond the Standard Model, we may even encounter magnetic monopoles along the way.
A magnetic monopole is a sink or a source of magnetic flux lines. It’s a point or region in space where magnetic flux is generated or annihilated. The magnetic flux lines, which are normally divergence-free but not necessarily closed, now have true endpoints at the monopole.
Sci-fi bonus: “Are monopoles connected to wormholes?”1
In particular, appearance of broken-up magnetic flux lines would yield a divergence term in the calculations:
This is forbidden in classical electrodynamics.
Specifically, that is because B can be written by applying the curl operator “∇×” to the magnetic vector potential A, which in turn is only allowed if B has no divergence term in the first place. Mathematically, this circular argument checks out as “∇· ∇×” being always zero.
The only exception to this rule (∇· ∇× A = 0) arises when the so-called symmetry of second derivates (Schwarz’s theorem) no longer applies. This happens in theories with multiply-connected topology (“singularities and wormholes”)2, or in theories defining electromagnetism using fields over a non-commutative algebra.
However, we have never ever observed magnetic monopoles in nature. Do we know why? No. We also don’t even know if we’re looking with the right instruments, since we haven’t agreed on a unified theory “of everything” yet.
The only thing we’re sure of is that fundamental physics in its current state arrived at multiple dead ends by now. This is why scientists and engineers are hunting for overlooked aspects or extensions to present-day theories, which may be leveraged for the good of humankind in the long-term.
Since beauty has always been a strong argument in mathematical physics—for whatever fundamental reasons—, researchers have a craving for those “tasty” monopoles, as they would then not only be allowed to use the really beautiful and symmetric version of Maxwell’s equations, but they also may be able to engineer the fabric of spacetime using those monopoles.
Dirac’s semi-classical solution
As we’ve learned in my previous article, the magnetic field is not really its own boss. Instead, it is derived from the magnetic vector potential. The magnetic vector potential is a vector field that globally captures (“encodes”) the direction and momentum of a localized electron current distribution.
I was wondering what the magnetic vector potential of a magnetic monopole would look like. We know that we can’t go backwards from B to A. And we know that B must be in a multiply-connected spacetime or over a non-commutative algebra. Moreover, one of the fundamental principles of physics—“gauge symmetry”—allows for vast freedom in deciding on any particular vector potential.
So what should the monopolar magnetic vector potential look like? This was mathematically worked out as a semi-classical theory by Paul Dirac (1902–1984) in 19313, so we don't need to reinvent it ourselves:
Here, the magnetic monopole is located at the origin (0, 0, 0), g is the magnetic charge, r and r are the vector and scalar distances from the origin respectively.
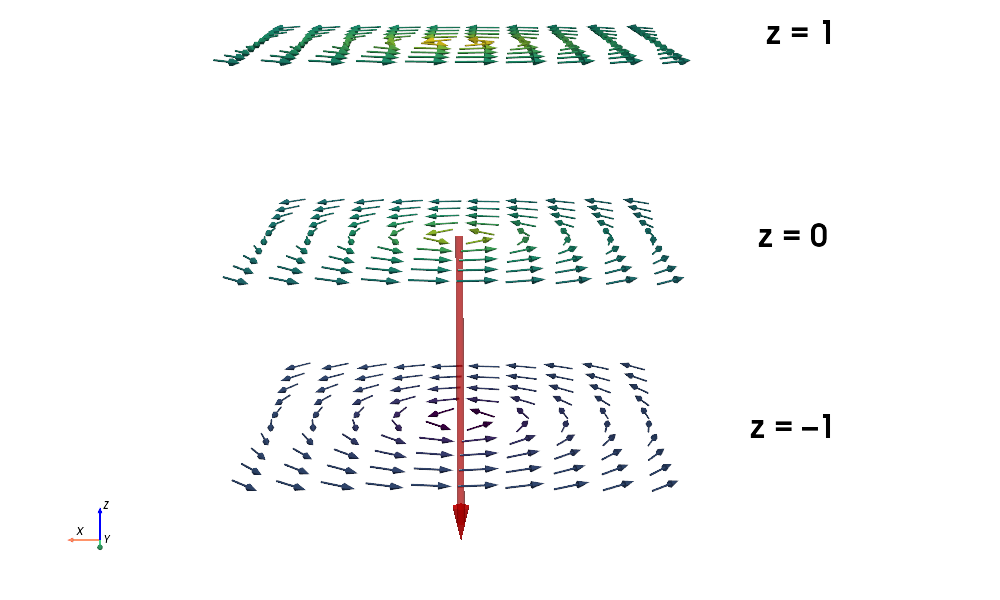
However, while the magnetic field of the magnetic monopole is isotropic (the same in all directions), the corresponding vector potential is not. Instead, the monopolar magnetic vector potential has a line singularity, which Dirac chose to put along the z-direction.
His expression for A is singular along the negative z-axis, producing the isotropic magnetic field everywhere—except at the origin (for r = 0), where the field itself becomes singular:
Yes, you read that right. We can still recover this monopolar magnetic field as the curl of the vector potential—even though the divergence of a curl is always zero in standard vector calculus. This only works because Dirac’s magnetic vector potential A is not smooth across all of space—it is singular along the negative z-axis, and undefined at the origin. As a result, the identity (∇· ∇× A = 0) no longer holds globally, allowing for a non-zero magnetic divergence.
This is one of those rare cases where classical field theory gets extended not by changing the laws, but by carefully examining the topology and smoothness of the fields involved. That’s how Dirac actually got away with breaking the rules.
Dirac’s monopolar magnetic vector potential is solenoidal—it actually looks like a B-field, except for the line singularity along the negative z-axis (shown here in red):
By now, I guess you're wondering how the magnetic monopole "knows" its location in space, while the monopolar magnetic vector potential A seems to looks the same everywhere along the z-axis.
The magic lies in the line singularity, which is an infinitesimally thin, one-directional defect where the magnetic vector potential is undefined. The magnetic monopole sits exactly at the free endpoint of that line, while the other end stretches off to infinity in an arbitrarily chosen direction (i.e., down the negative z-axis in Dirac's solution).
The resulting monopolar magnetic field B, however, doesn't care about the direction of the string — only about where it begins, with B diverging from the free end of the line singularity like this:
Now, could we detect magnetic monopoles by their vector potential, as shown above? Yes, in principle. Quantum interference allows us to measure not A itself, but path-dependent differences in A4—possibly just enough to reveal a hidden monopole, or at least traces of interfering monopolar magnetic vector potentials.
Engineers and scientists are probing the limits of electrodynamics and of physics beyond the Standard Model today, developing tomorrow's tools to hunt the hidden vector potential and engineer the fabric of spacetime itself.
The godfather field
Did you know that the mystery of the magnetic vector potential is even deeper than “just” being the background for magnetic monopoles? Today’s physicists realize that it directly manipulates the phase terms of wave functions, i.e. of “everything”. This is a strong argument for the magnetic vector potential being more fundamental than the magnetic field.
Moreover, the magnetic vector potential should be polarizable freely into arbitrary field configurations. But that would imply that Maxwell's equations are just a subset of a more general electrodynamics where an arbitrarily engineered vector potential should generate non-classical B-fields5, e.g. ones with multiply-connected topology.
Shaping the magnetic vector potential A may give us total freedom over the topology of magnetism, finally tapping into those “tasty” magnetic monopoles.
The magnetic vector potential might actually be the “most valuable player” among fields—defining not just wave functions, but possibly spacetime itself.
Join the discussion—subscribe and comment below.
Follow @drxwilhelm on X Twitter, Substack, Bluesky, Discord, and YouTube. (About)
The source code used to generate the graphics in this article is in the public domain.
https://patents.google.com/patent/US20060168937A1/en
A “multiply-connected” spacetime is one where certain loops cannot be continuously shrunk to a point without leaving the space.
https://en.wikipedia.org/wiki/Magnetic_monopole#Quantum_mechanics
The magnetic vector potential is measurable in quantum interference experiments like the one done by R. G. Chambers in 1960 that verified the so-called Aharonov-Bohm effect.
There are approaches to higher-symmetry electrodynamics, e.g. SU(2) electrodynamics by T.W. Barrett; he makes a strong case for the existence and experimental validation of his theory, but doesn’t seem to give its explicit operator-valued form.